An interactive graphical simulation of nucleic acid polymerases
Disclaimer: SimPol is currently in prerelease. It has not been peer-reviewed or published.
SimPol is a free open-source web-based program aimed to help researchers, teachers and students visualise transcription. Transcription is an essential pathway for all living organisms. It involves the copying of a template, typically DNA, into messenger RNA (mRNA) which is used to produce protein. Transcription is carried out by an enzyme called RNA polymerase. This webpage contains tutorials about SimPol and is hopefully friendly to all users.
Contents
| Loading... |
Getting Started
Information icons
Help icons
 are scattered throughout the interface of SimPol. Pressing one of these buttons will redirect to
the relevant section on this page.
are scattered throughout the interface of SimPol. Pressing one of these buttons will redirect to
the relevant section on this page.
Conversely, there are direct links from this page to SimPol which look like this: Example session: Open | View XML The XML files that specify the session parameters can be downloaded or the session can be directly opened.
Sequence selection
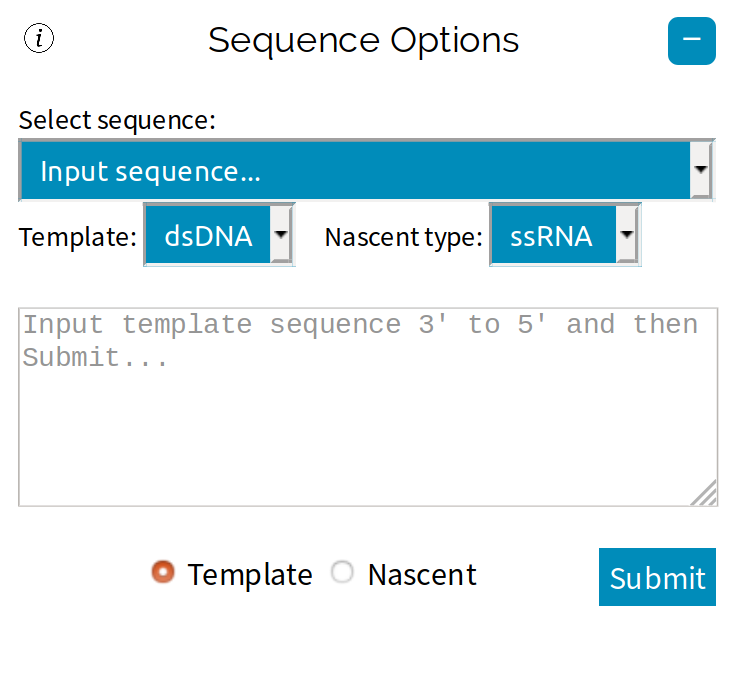
To enter a nucleic acid sequence, open up the ☰ Parameters side-navigation menu, under "Select sequence" choose "Input sequence", enter a sequence and then press Submit.
A range of example sequences have also been provided.
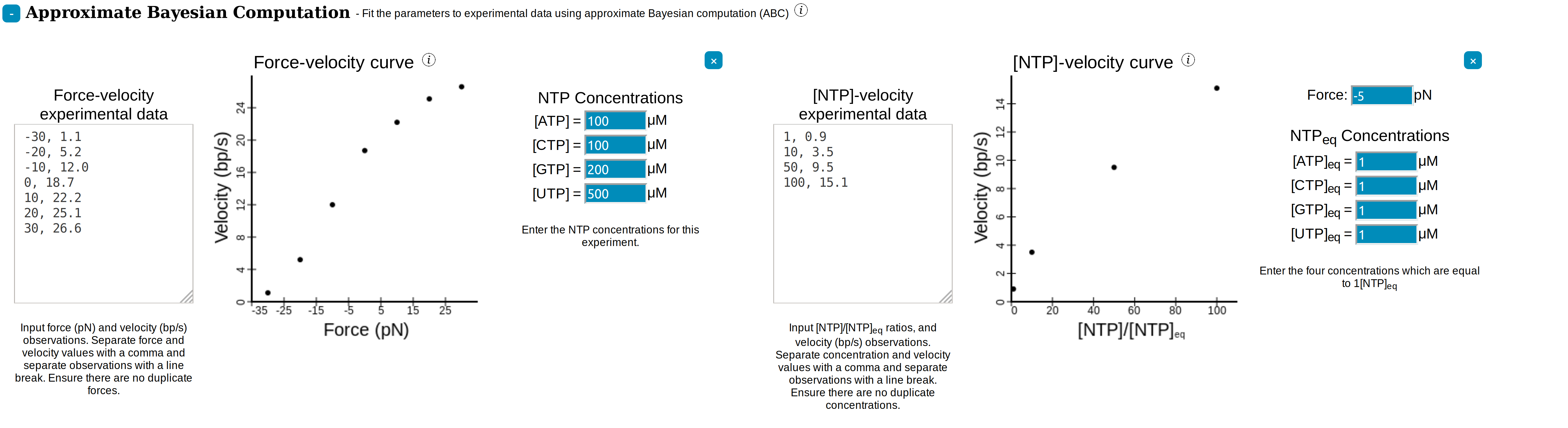
SimPol is designed primarily for transcription with DNA-dependent RNA-polymerases. The choice of template-type (DNA or RNA) and nascent-type (DNA or RNA) will dictate
which thermodynamic parameters are used - Turner's RNA/RNA parameters, Sugimoto's DNA/RNA parameters, or SantaLucia's DNA/DNA parameters.
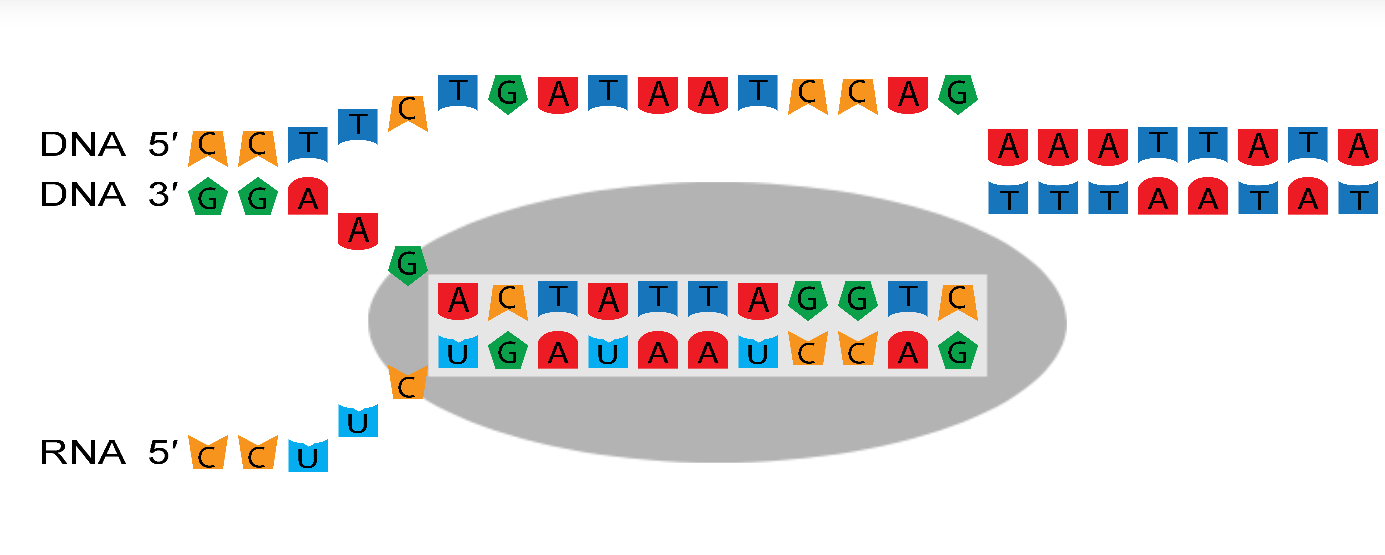
Polymerase structure
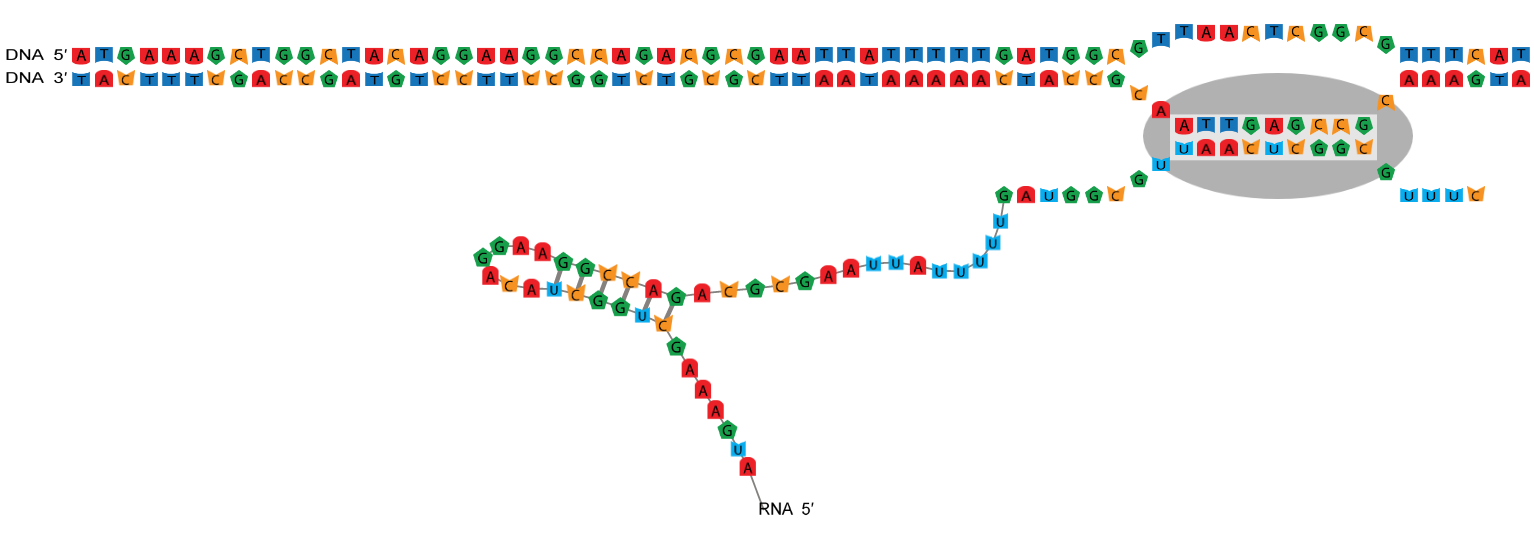
RNA polymerases reads the template strand (the gene) in the 3′ → 5′ direction, and copies it to create the nascent strand (the mRNA) which grows in the 5′ → 3′ direction.
The transcription bubble consists of a hybrid between the nascent strand and the template strand within the polymerase, and a set of unpaired
template bases upstream and downstream of the polymerase. In this example, the transcription bubble contains 2 + 11 + 0 = 13 bp.
The size of the transcription bubble differs between polymerases. These three parameters have a large effect on the sequence-dependent properties of the enzyme and can be changed from the ☰ Parameters side-navigation menu.
The size of the transcription bubble differs between polymerases. These three parameters have a large effect on the sequence-dependent properties of the enzyme and can be changed from the ☰ Parameters side-navigation menu.

The toolbar
 |
 |

|
 |
 |
 |
|
N =
|
|
|
|
|
 |

|

|
|
The toolbar contains a range of essential functions.
Reinitiate resets the enzyme to its initial position. This will
not affect plots or any other outputs. If any parameters have prior distributions then they will be resampled.
resets the enzyme to its initial position. This will
not affect plots or any other outputs. If any parameters have prior distributions then they will be resampled.
Stop immediately halts any polymerase acitivies taking place.
This will not affect any parameters, plots or other outputs.
immediately halts any polymerase acitivies taking place.
This will not affect any parameters, plots or other outputs.
N = is a variable. The meaning of N depends on which tool is being used.
Simulate begins the random simulation starting from the current position
of the polymerase. During the simulation, reactions are
randomly sampled according to their rate constants, which can be tweaked in the parameters menu. N trials are performed in the simulation. When the polymerase
finishes copying the sequence (or prematurely terminates) the next trial begins. The animation time of each reaction in the simulation is determined by Speed.
The simulation can be stopped early using the Stop
begins the random simulation starting from the current position
of the polymerase. During the simulation, reactions are
randomly sampled according to their rate constants, which can be tweaked in the parameters menu. N trials are performed in the simulation. When the polymerase
finishes copying the sequence (or prematurely terminates) the next trial begins. The animation time of each reaction in the simulation is determined by Speed.
The simulation can be stopped early using the Stop  button.
button.
Clear cache opens up a dialog to allow the deletion of any kinetic or sequence data which has been saved
during the simulation. The kinetic data is displayed in plots so think of this button as resetting the plots.
opens up a dialog to allow the deletion of any kinetic or sequence data which has been saved
during the simulation. The kinetic data is displayed in plots so think of this button as resetting the plots.
Copy transcribes/replicates/copies the next N bases. The animation time is determined by Speed.
Copying can be stopped early using the Stop
transcribes/replicates/copies the next N bases. The animation time is determined by Speed.
Copying can be stopped early using the Stop  button.
button.
Stutter copies the current base N times, therefore adding an insertion of
size N into the nascent strand. Insertions are added through slippage. The animation time is determined by Speed.
Stuttering can be stopped early using the Stop button.
copies the current base N times, therefore adding an insertion of
size N into the nascent strand. Insertions are added through slippage. The animation time is determined by Speed.
Stuttering can be stopped early using the Stop button.
Fold folds the mRNA into its predicted secondary structure and renders the predicted structure. This function will only work
if the nascent strand is single-stranded RNA. Note that this function is only cosmetic and will not affect the polymerase's kinetics. To incorporate mRNA secondary structure predictions into the kinetic model
see . Folding is performed by the ViennaRNA suite.
folds the mRNA into its predicted secondary structure and renders the predicted structure. This function will only work
if the nascent strand is single-stranded RNA. Note that this function is only cosmetic and will not affect the polymerase's kinetics. To incorporate mRNA secondary structure predictions into the kinetic model
see . Folding is performed by the ViennaRNA suite.
Speed is a variable which controls the speed of the animation while Copying, Stuttering or Simulating. If the speed is set to slow, medium or fast, then the polymerase will animate each reaction at a slow, medium or fast speed, respectively. If the speed is hidden, then the polymerase is no longer displayed and will not animate at all. The plots will update periodically. Hidden is the fastest setting.
Save downloads the current session in XML format. If the page is refreshed or if your web browser crashes the settings will be lost.
downloads the current session in XML format. If the page is refreshed or if your web browser crashes the settings will be lost.
Load uploads a saved XML session file.
uploads a saved XML session file.
Reinitiate
 resets the enzyme to its initial position. This will
not affect plots or any other outputs. If any parameters have prior distributions then they will be resampled.
resets the enzyme to its initial position. This will
not affect plots or any other outputs. If any parameters have prior distributions then they will be resampled. Stop
 immediately halts any polymerase acitivies taking place.
This will not affect any parameters, plots or other outputs.
immediately halts any polymerase acitivies taking place.
This will not affect any parameters, plots or other outputs. N = is a variable. The meaning of N depends on which tool is being used.
Simulate
 begins the random simulation starting from the current position
of the polymerase. During the simulation, reactions are
randomly sampled according to their rate constants, which can be tweaked in the parameters menu. N trials are performed in the simulation. When the polymerase
finishes copying the sequence (or prematurely terminates) the next trial begins. The animation time of each reaction in the simulation is determined by Speed.
The simulation can be stopped early using the Stop
begins the random simulation starting from the current position
of the polymerase. During the simulation, reactions are
randomly sampled according to their rate constants, which can be tweaked in the parameters menu. N trials are performed in the simulation. When the polymerase
finishes copying the sequence (or prematurely terminates) the next trial begins. The animation time of each reaction in the simulation is determined by Speed.
The simulation can be stopped early using the Stop  button.
button. Clear cache
 opens up a dialog to allow the deletion of any kinetic or sequence data which has been saved
during the simulation. The kinetic data is displayed in plots so think of this button as resetting the plots.
opens up a dialog to allow the deletion of any kinetic or sequence data which has been saved
during the simulation. The kinetic data is displayed in plots so think of this button as resetting the plots. Copy
 transcribes/replicates/copies the next N bases. The animation time is determined by Speed.
Copying can be stopped early using the Stop
transcribes/replicates/copies the next N bases. The animation time is determined by Speed.
Copying can be stopped early using the Stop  button.
button. Stutter
 copies the current base N times, therefore adding an insertion of
size N into the nascent strand. Insertions are added through slippage. The animation time is determined by Speed.
Stuttering can be stopped early using the Stop button.
copies the current base N times, therefore adding an insertion of
size N into the nascent strand. Insertions are added through slippage. The animation time is determined by Speed.
Stuttering can be stopped early using the Stop button. Fold
 folds the mRNA into its predicted secondary structure and renders the predicted structure. This function will only work
if the nascent strand is single-stranded RNA. Note that this function is only cosmetic and will not affect the polymerase's kinetics. To incorporate mRNA secondary structure predictions into the kinetic model
see . Folding is performed by the ViennaRNA suite.
folds the mRNA into its predicted secondary structure and renders the predicted structure. This function will only work
if the nascent strand is single-stranded RNA. Note that this function is only cosmetic and will not affect the polymerase's kinetics. To incorporate mRNA secondary structure predictions into the kinetic model
see . Folding is performed by the ViennaRNA suite. Speed is a variable which controls the speed of the animation while Copying, Stuttering or Simulating. If the speed is set to slow, medium or fast, then the polymerase will animate each reaction at a slow, medium or fast speed, respectively. If the speed is hidden, then the polymerase is no longer displayed and will not animate at all. The plots will update periodically. Hidden is the fastest setting.
Save
 downloads the current session in XML format. If the page is refreshed or if your web browser crashes the settings will be lost.
downloads the current session in XML format. If the page is refreshed or if your web browser crashes the settings will be lost. Load
 uploads a saved XML session file.
uploads a saved XML session file.
States and Reactions
Kinetic model of transcription
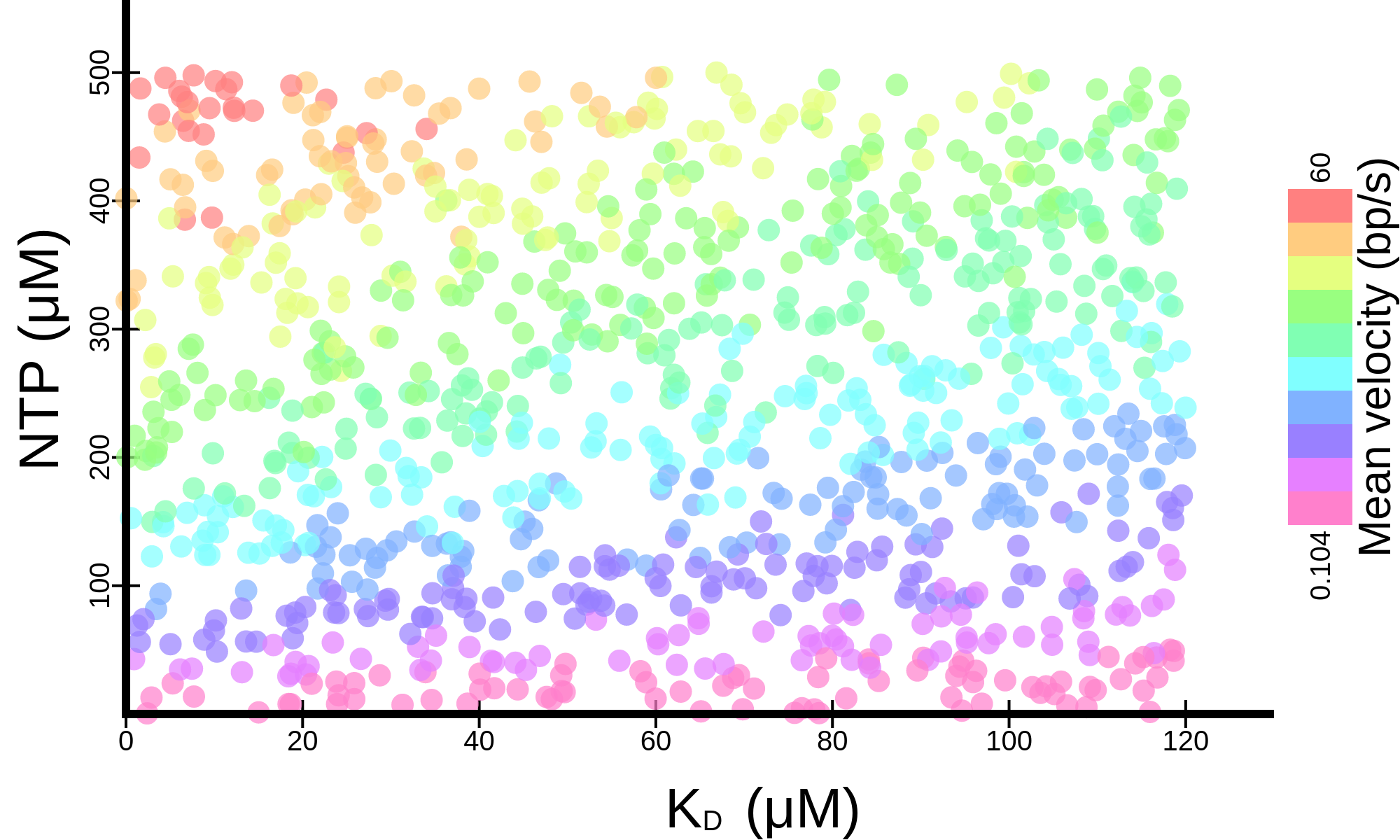
Let $S(l,t)$ denote the current state, where $l$ is the length of the mRNA and $t$ is the position of the RNA polymerase (RNAP) active site with respect to the $3^\prime$ mRNA. Under the Brownian ratchet model, transcription elongation is a three step cycle. First, RNAP translocates from the pretranslocated position $S(l,0)$ into the posttranslocated position $S(l,1)$. Second, the incoming nucleoside triphosphate (NTP) binds to the active site of RNAP, $S_N(l,1)$. Finally, the bound NTP is incorporated onto the $3^\prime$ mRNA, returning the RNAP into the pretranslocated position $S(l+1,0)$.
However, RNAP does not always conform to this pathway. Periodically, RNAP backtracks ($t < 0$), whereby the enzyme translocates upstream causing the $3^\prime$ mRNA to exit through the NTP entry channel. This renders the enzyme catalytically inactive. It has been hypothesised that an intermediate state (IS) acts as a precursor for backtracking from the pretranslocated state. Alternatively, RNAP can hypertranslocate ($t>1$), whereby the enzyme translocates further downstream causing the shortening of the DNA/RNA hybrid.
Kinetic diagram
Hover over a state read its description.
In SimPol, backtracking, hypertranslocation, and the IS can each be enabled or disabled from the ☰ Parameters side-navigation menu. The kinetic diagram of the current model can be viewed using . Pressing the simulate button
 simulates the system according to the
currently specified pathway. See
Simulating.
simulates the system according to the
currently specified pathway. See
Simulating.
Reactions
The polymerase can be controlled manually using the Navigation panel at the top of the main page.
Translocation:
There are two translocation reactions: Backwards and Forwards. These operations move the polymerase one position left and right respectively, with respect to the
template and nascent strand. These operations involve reconfiguring the base-pairs within the hybrid, and within the gene if it is double-stranded. If the polymerase moves beyond the 3′ end of the nascent strand (ie. hypertranslocation),
then the nascent strand will be released (termination).
Hotkeys: ← and → arrow keys
Nucleotide incorporation:
If the active site is free and next to the 3′ end of the nascent strand, then the polymerase may bind NTP.
Once bound, the polymerase may catalyse the reaction, or it may release the NTP back into the cell. Reverse-catalysis may also be performed
(Lysis), although this reaction is often considered to be irreversible. The canonical pathway of transcription
elongation is a three step cycle: 1) forward translocation, 2) NTP binding, 3) catalysis. This may also be achieved with the Copy
 function.
Hotkeys: Shift + ← and → arrow keys
function.
Hotkeys: Shift + ← and → arrow keys
 function.
Hotkeys: Shift + ← and → arrow keys
function.
Hotkeys: Shift + ← and → arrow keys
Inactivation:
It is hypothesised that the catalytically inactive intermediate state, IS, acts as a precursor for backtracking. The Deactivate reaction causes the
polymerase to enter the IS from the pretranslocated state, thus enabling backtracking to occur. The Activate reaction is the reverse.
Cleavage:
When a nucleic acid polymerase backtracks for too long in vivo it can delay the production of its product and potentially cause roadblocks for other polymerases.
Many organisms have evolved elongation factors which serve to rescue the polymerase from this state. One mechanism these factors may act is by cleaving the 3′
end of the nascent strand when it pokes out the front of the polymerase during backtracking. This is carried out by GreA and GreB for prokaryotic
RNA polymerases and S-II for eukaryotic RNA polymerase II and can be performed in SimPol using the cleavage reaction.
Slippage:
During slippage, one strand in the (DNA/RNA) hybrid moves with respect to the other (ie. they slip along each other).
Slippage is a key mechanism of insertion and deletion. In SimPol, this can be initialised using the Form Bulge reaction.
When this happens, a nucleotide bulge forms within the duplex. This can occur within either the template or nascent strand (however in SimPol it can currently only occur within the nascent strand). When a bulge forms,
the active site may be opened up, allowing one of the template bases to be copied twice. This would lead to an insertion. The bulge may
diffuse left or right along the
hybrid. This process is favoured if the hybrid sequence is repetitive (eg. AAAAAAAAA/UUUUUUUUU). When positioned at either end of the hybrid, the bulge may be absorbed. This three step process (bulge formation, diffusion and absorption)
is based off the models proposed by Neher et al. and is believed to be the mechanism behind transcriptional slippage. Iterative slippage and elongation can lead to large insertions. This is sometimes called stuttering and
can also be achieved with the Stutter  function.
Hotkeys: Ctrl + ← and → arrow keys
function.
Hotkeys: Ctrl + ← and → arrow keys
 function.
Hotkeys: Ctrl + ← and → arrow keys
function.
Hotkeys: Ctrl + ← and → arrow keys
 button. The raw data (.tsv) or a high resolution image (.png) can be downloaded
button. The raw data (.tsv) or a high resolution image (.png) can be downloaded  . The different
plots available are detailed below.
. The different
plots available are detailed below.
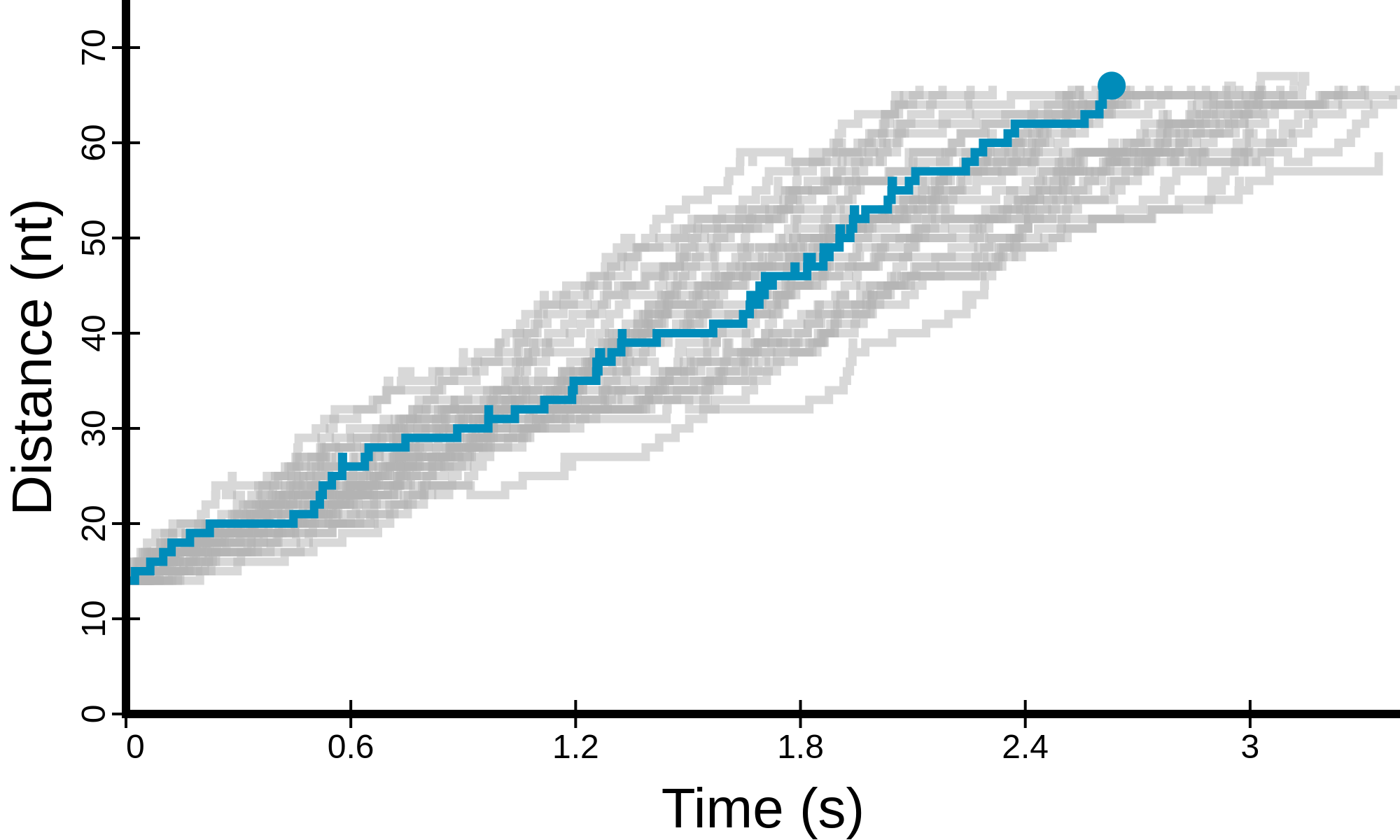
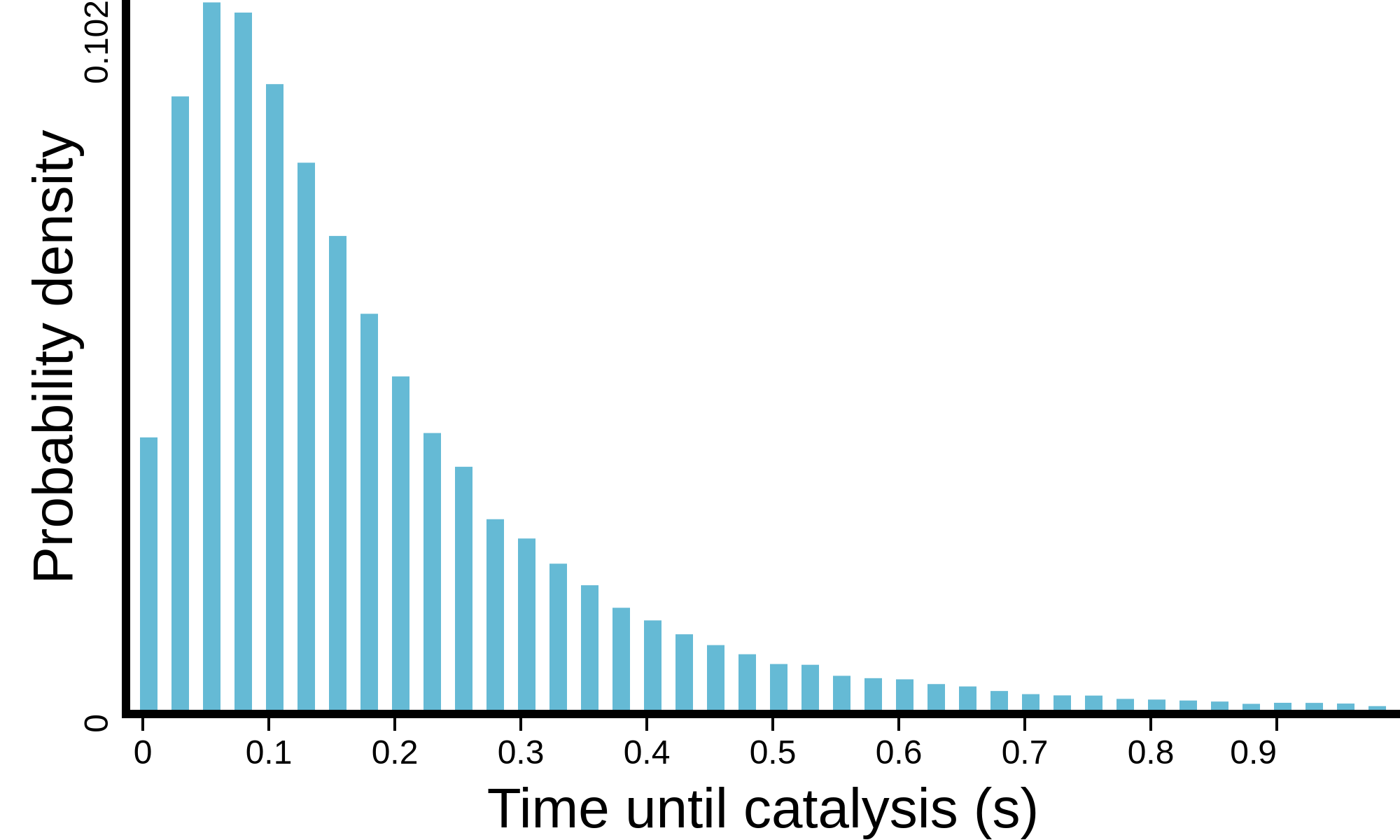
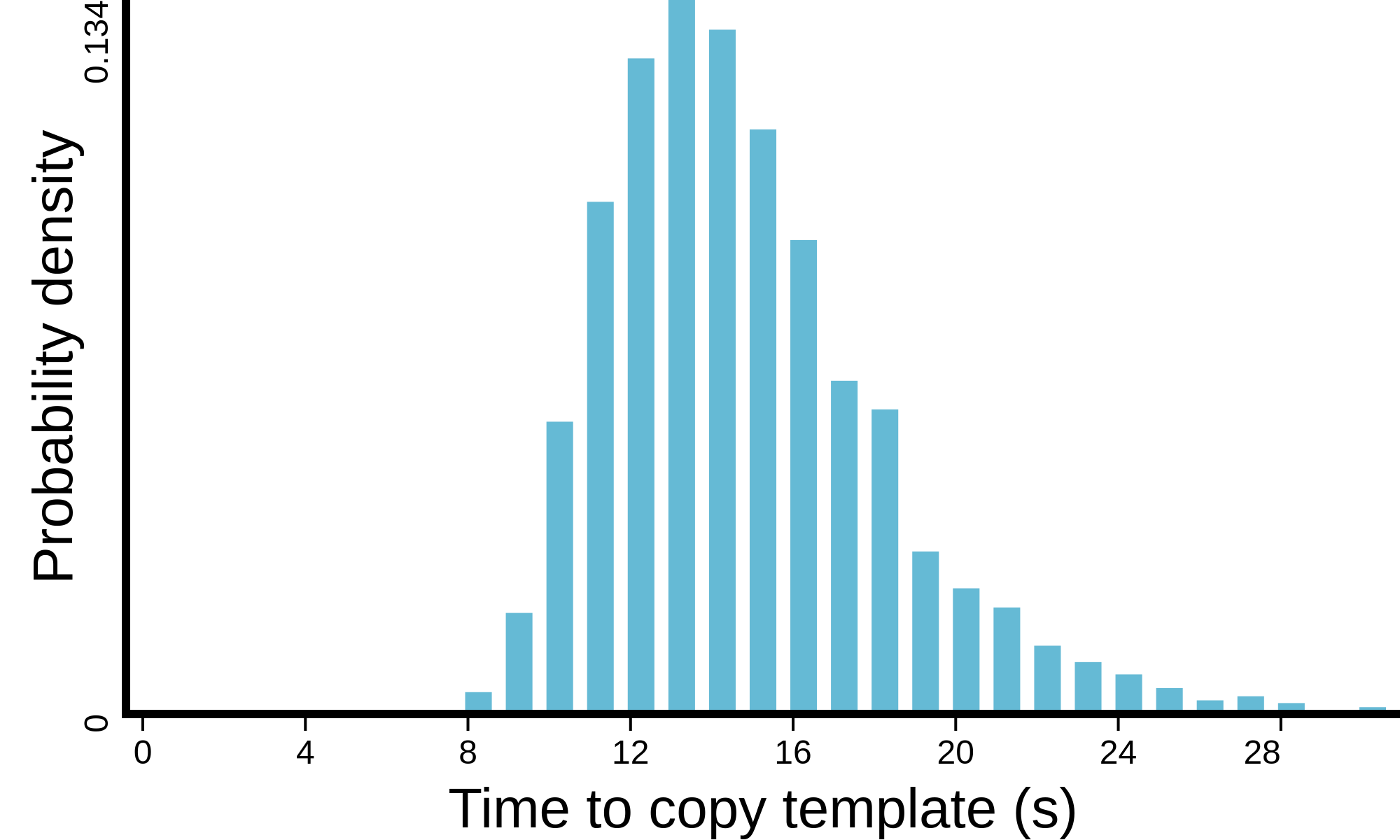
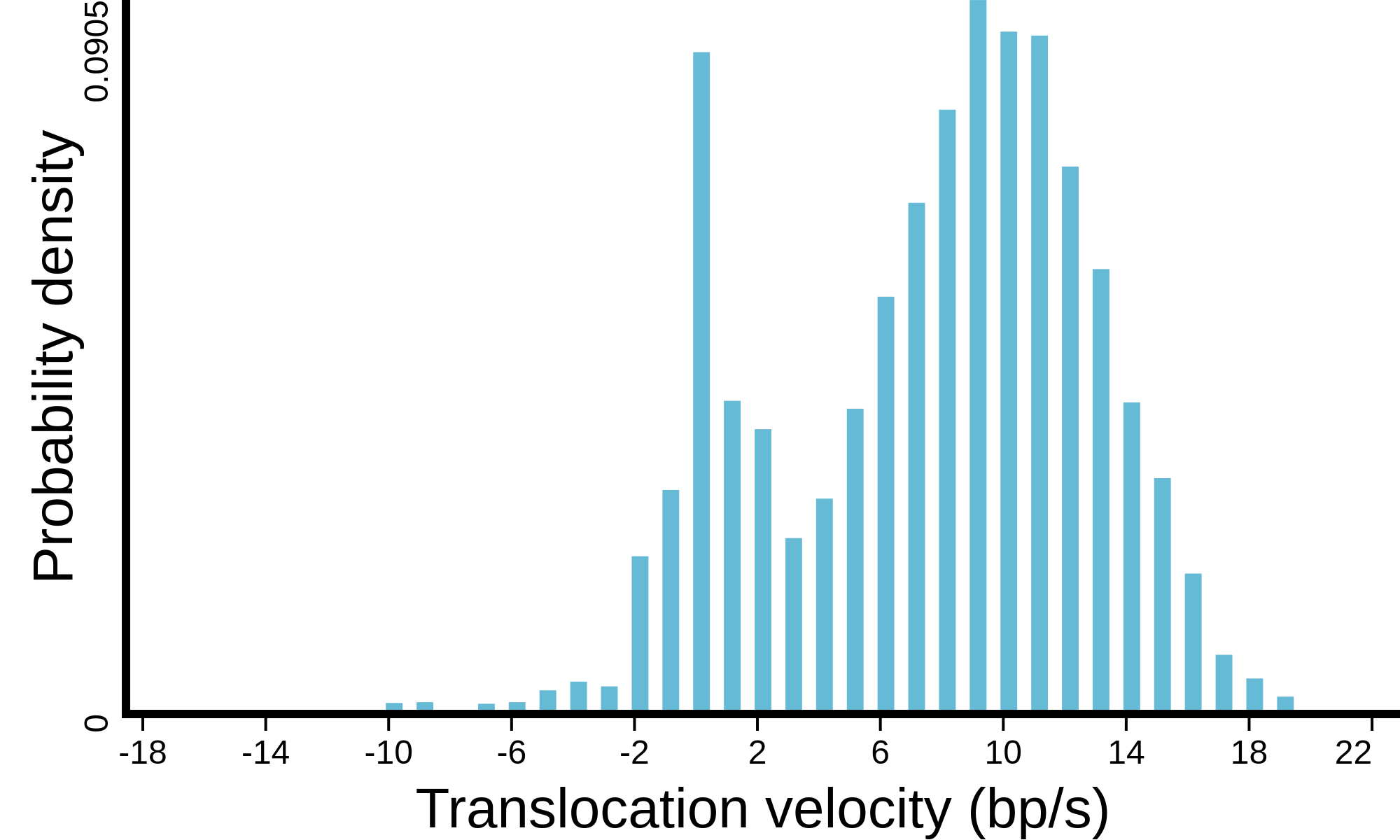
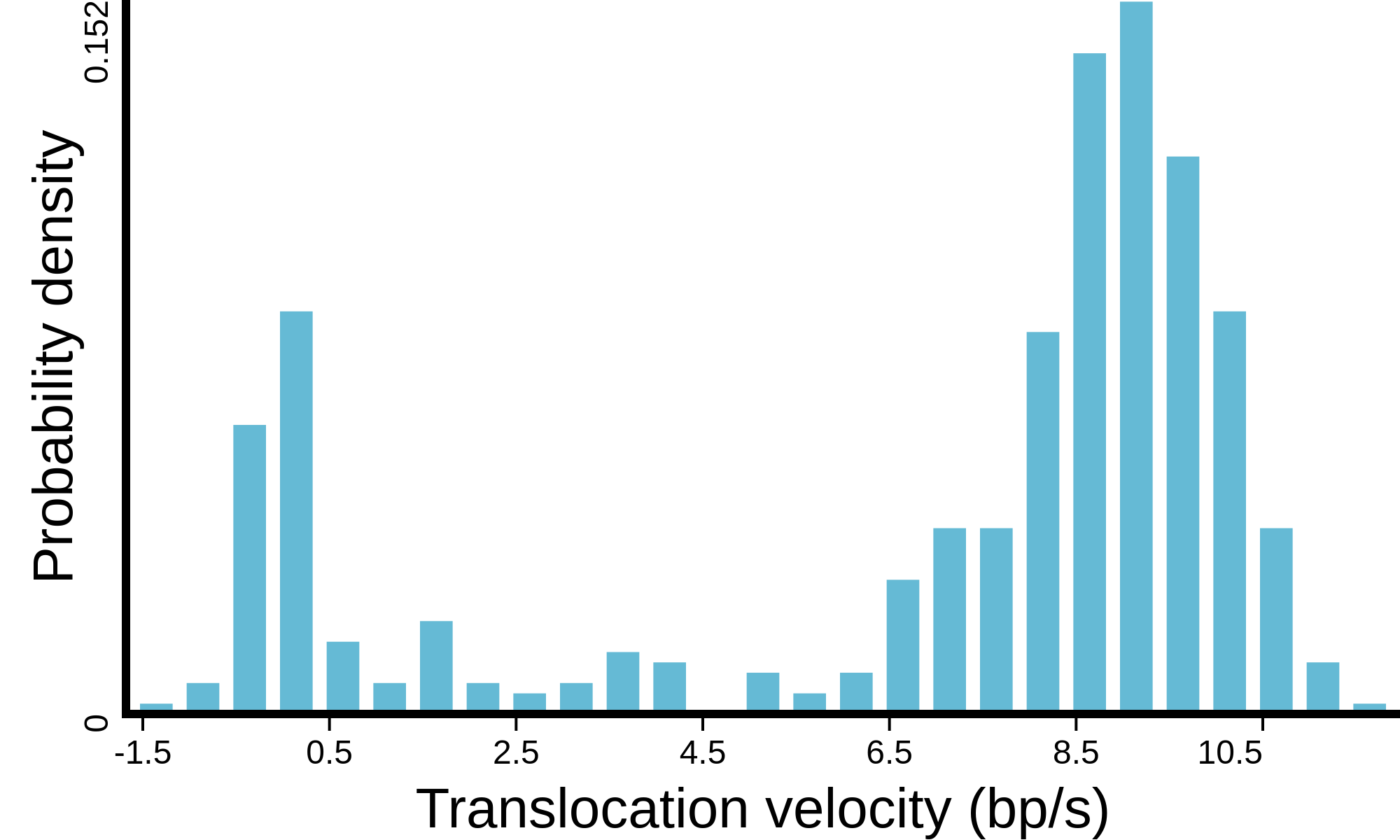
 (see
(see